Time-structure Independent Components Analysis (tICA)¶

Background¶

tICA compared to PCA (courtesy of C. R. Schwantes)

Time-structure independent components analysis (tICA) is a method for finding the slowest-relaxing degrees of freedom in a time series data set which can be formed from linear combinations from a set of input degrees of freedom.

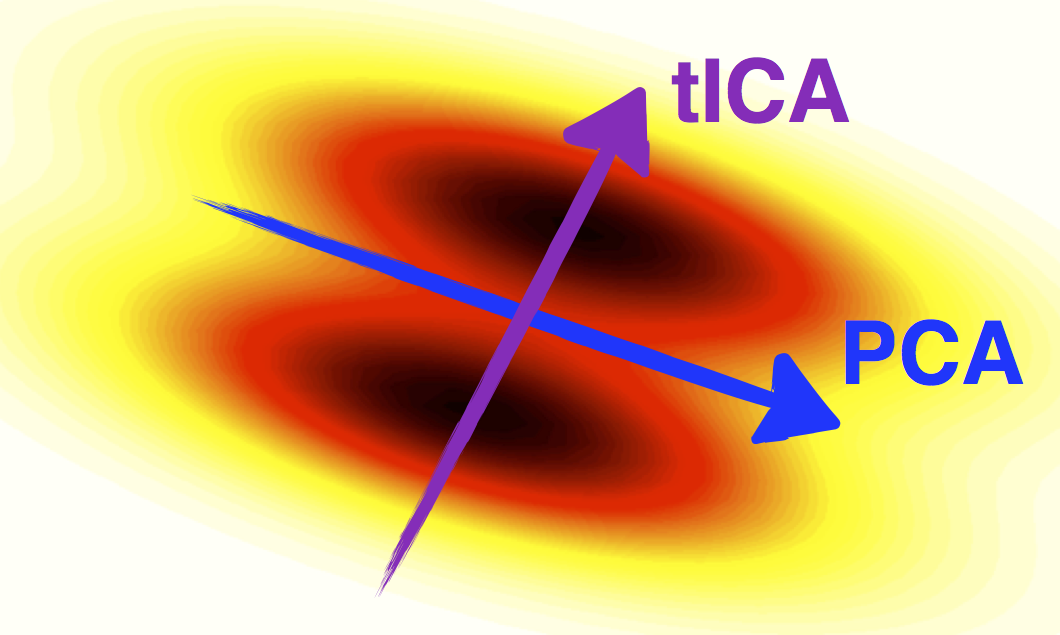
tICA can be used as a dimensionality reduction method, and in that capacity it is somewhat similar to PCA. However whereas PCA finds high-variance linear combinations of the input degrees of freedom, tICA finds high-autocorrelation linear combinations of the input degrees of freedom.

Algorithms¶

Combination with MSM¶

While the tICs are themselves approximations to the dominant eigenfunctions of the propagator / transfer operator, the approach taken in [1] and [2] is to “stack” tICA with Markov state models (MSMs). For example, in [2], Perez-Hernandez et al. first measured the 66 atom-atom distances between a set of atoms in each frame of their MD trajectories, and then use tICA to find the slowest 1, 4, and 10 linear combinations of these degrees of freedom and transform the 66-dimensional dataset into a 1, 4, or 10-dimensional dataset. Then, they apply KMeans to the resulting data and build an MSM.

Example¶

from msmbuilder.decomposition import tICA
from msmbuilder.cluster import KMeans
from msmbuilder.msm import MarkovStateModel
from sklearn.pipeline import Pipeline

pipeline = Pipeline([
    ('tica', tICA(n_components=4)),
    ('kmeans', KMeans(n_clusters=1000)),
    ('msm': MarkovStateModel(),
])

# load a list of 2D arrays, each of shape (length_of_trajectory, n_features)
dataset = ...

pipeline.fit(dataset)

References¶