API Intro: FS PeptideΒΆ

Modeling dynamics of FS Peptide

This example shows a typical, basic usage of MSMBuilder to model dynamics of a protein system.

MSMBuilder includes example datasets

The following cell downloads an example protein dataset to ~/msmbuilder_data. In practice, you will generate your own dataset by running molecular dynamics (MD) on your system of interest. MSMBuilder does not run MD.

In [1]:
# Download example dataset
from msmbuilder.example_datasets import FsPeptide
fs_peptide = FsPeptide()
fs_peptide.cache()
In [2]:
# Work in a temporary directory
import tempfile
import os
os.chdir(tempfile.mkdtemp())

The dataset object

MD datasets are usually quite large. It doesn't make sense to load everything into memory at once. The dataset object lazily-loads trajectories as they are needed. Below, we create a dataset out of the 28 *.xtc files we downloaded above. Since the data was saved at 50 ps / frame, we only load every 10th frame (with a new frequency of 0.5/ns).

In [3]:
from msmbuilder.dataset import dataset
xyz = dataset(fs_peptide.data_dir + "/*.xtc",
              topology=fs_peptide.data_dir + '/fs-peptide.pdb',
              stride=10)
print("{} trajectories".format(len(xyz)))
# msmbuilder does not keep track of units! You must keep track of your
# data's timestep
to_ns = 0.5
print("with length {} ns".format(set(len(x)*to_ns for x in xyz)))

/home/travis/miniconda3/envs/docenv/lib/python3.5/site-packages/mdtraj/formats/pdb/pdbfile.py:196: UserWarning: Unlikely unit cell vectors detected in PDB file likely resulting from a dummy CRYST1 record. Discarding unit cell vectors.
  warnings.warn('Unlikely unit cell vectors detected in PDB file likely '

28 trajectories
with length {500.0} ns

Featurization

The raw (x, y, z) coordinates from the simulation do not respect the translational and rotational symmetry of our problem. A Featurizer transforms cartesian coordinates into other representations. Here we use the DihedralFeaturizer to turn our data into phi and psi dihedral angles. Observe that the 264*3-dimensional space is reduced to 84 dimensions

In [4]:
from msmbuilder.featurizer import DihedralFeaturizer
featurizer = DihedralFeaturizer(types=['phi', 'psi'])
diheds = xyz.fit_transform_with(featurizer, 'diheds/', fmt='dir-npy')

print(xyz[0].xyz.shape)
print(diheds[0].shape)

(1000, 264, 3)
(1000, 84)

Intermediate kinetic model: tICA

tICA is similar to principal component analysis (see "tICA vs. PCA" example). Note that the 84-dimensional space is reduced to 4 dimensions.

In [5]:
from msmbuilder.decomposition import tICA
tica_model = tICA(lag_time=2, n_components=4)
# fit and transform can be done in seperate steps:
tica_model = diheds.fit_with(tica_model)
tica_trajs = diheds.transform_with(tica_model, 'ticas/', fmt='dir-npy')

print(diheds[0].shape)
print(tica_trajs[0].shape)

(1000, 84)
(1000, 4)

tICA Heatmap

We can histogram our data projecting along the two slowest degrees of freedom (as found by tICA)

In [6]:
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
txx = np.concatenate(tica_trajs)
plt.hexbin(txx[:,0], txx[:,1], bins='log', mincnt=1, cmap='viridis')

/home/travis/miniconda3/envs/docenv/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
  warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')
/home/travis/miniconda3/envs/docenv/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
  warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')
Out[6]:
<matplotlib.collections.PolyCollection at 0x2b6dbff82748>

Clustering

Conformations need to be clustered into states (sometimes written as microstates). We cluster based on the tICA projections to group conformations that interconvert rapidly. Note that we transform our trajectories from the 4-dimensional tICA space into a 1-dimensional cluster index.

In [7]:
from msmbuilder.cluster import MiniBatchKMeans
clusterer = MiniBatchKMeans(n_clusters=100)
clustered_trajs = tica_trajs.fit_transform_with(
    clusterer, 'kmeans/', fmt='dir-npy'
)

print(tica_trajs[0].shape)
print(clustered_trajs[0].shape)

(1000, 4)
(1000,)
In [8]:
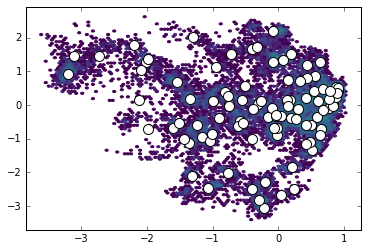
plt.hexbin(txx[:,0], txx[:,1], bins='log', mincnt=1, cmap='viridis')
plt.scatter(clusterer.cluster_centers_[:,0],
            clusterer.cluster_centers_[:,1], 
            s=100, c='w')
Out[8]:
<matplotlib.collections.PathCollection at 0x2b6dbe245358>

MSM

We can construct an MSM from the labeled trajectories

In [9]:
from msmbuilder.msm import MarkovStateModel
from msmbuilder.utils import dump
msm = MarkovStateModel(lag_time=2, n_timescales=20)
msm.fit(clustered_trajs)

MSM contains 2 strongly connected components above weight=0.50. Component 1 selected, with population 96.478672%
Out[9]:
MarkovStateModel(ergodic_cutoff='on', lag_time=2, n_timescales=20,
         prior_counts=0, reversible_type='mle', sliding_window=True,
         verbose=True)
In [10]:
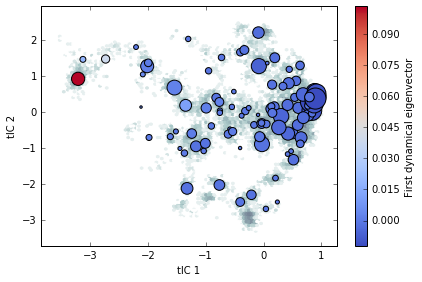
plt.hexbin(txx[:, 0], txx[:, 1], bins='log', mincnt=1, cmap="bone_r")
plt.scatter(clusterer.cluster_centers_[msm.state_labels_, 0],
            clusterer.cluster_centers_[msm.state_labels_, 1],
            s=1e4 * msm.populations_,       # size by population
            c=msm.left_eigenvectors_[:, 1], # color by eigenvector
            cmap="coolwarm") 
plt.colorbar(label='First dynamical eigenvector')
plt.xlabel('tIC 1')
plt.ylabel('tIC 2')
plt.tight_layout()
In [11]:
msm.timescales_
Out[11]:
array([ 1030.70240747,   851.47838408,   654.29040131,   364.0700632 ,
         285.96878774,   275.24863097,   194.65385388,   166.37677322,
         135.75320939,   112.44480139,    96.66953408,    82.83449429,
          81.14871343,    78.94464901,    69.14149203,    65.661408  ,
          57.80688991,    56.22141773,    52.3080546 ,    51.36146463])
In [12]:
plt.subplots(figsize=(3,5))
plt.hlines(msm.timescales_ * to_ns, 0, 1, color='b')
plt.yscale('log')
plt.xticks([])
plt.ylabel("Timescales / ns", fontsize=18)
plt.tight_layout()

Macrostate Model

In [13]:
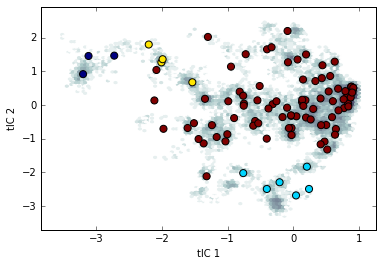
from msmbuilder.lumping import PCCAPlus
pcca = PCCAPlus.from_msm(msm, n_macrostates=4)
macro_trajs = pcca.transform(clustered_trajs)

Optimization terminated successfully.
         Current function value: -3.988377
         Iterations: 8
         Function evaluations: 87
In [14]:
plt.hexbin(txx[:, 0], txx[:, 1], bins='log', mincnt=1, cmap="bone_r")
plt.scatter(clusterer.cluster_centers_[msm.state_labels_, 0],
            clusterer.cluster_centers_[msm.state_labels_, 1],
            s=50,
            c=pcca.microstate_mapping_,
)
plt.xlabel('tIC 1')
plt.ylabel('tIC 2')
Out[14]:
<matplotlib.text.Text at 0x2b6dcb195cf8>

(Intro.ipynb; Intro_eval.ipynb; Intro.py)